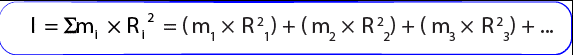Pada kesempatan kali ini pengajar.co.id akan menciptakan postingan mengenai Momen Inersia , yuk sama-sama kita bahas dibawah ini :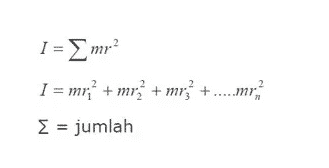
Pengertian Momen Inersia
Dalam aturan pertama Newton dibilang “objek bergerak akan condong bergerak dan benda tetap condong damai.” Selain itu, inersia adalah kecenderungan benda untuk menjaga negara (hanya diam atau mampu bergerak). Inersia juga disebut inersia dari suatu objek. Oleh karena itu, hukum pertama Newton, juga dikenal selaku hukum inersia atau hukum inersia. Sebagai acuan, benda-benda yang sulit untuk bergerak dikatakan memiliki inersia yang besar. Rotasi bumi senantiasa dalam keadaan yang disebut mempunyai rotasi insersia.
Saat atau momen gaya yakni produk dari kekuatan lengan momen. Jadi, momen inersia yakni ukuran kecenderungan atau inersia dari benda berputar pada porosnya.
Ukuran saat obyek inersia dipengaruhi oleh beberapa aspek, mirip:
- massa benda
- Bentuk (geometri)
- Lokasi sumbu rotasi
- Jarak dari sumbu rotasi dari objek (lengan tuas).
Momen Inersia Partikel
Sebelum mendekati momen inersia dari benda tegar, pertama kita mesti mencar ilmu momen inersia partikel. dalam hal ini, tidak membayangkan partikel objek yang sungguh kecil. Bahkan, tidak ada batas ukuran untuk partikel kata. Dengan demikian, penggunaan partikel jangka panjang untuk memfasilitasi pembahasan gerak, di mana posisi objek digambarkan selaku posisi sebuah titik. Konsep partikel-partikel ini yang kita gunakan dalam pembahasan gerak benda pada Kinematika topik (motion linear, Parabolic Gerak, gerakan melingkar) dan dinamis (hukum Newton). Dengan demikian, objek yang dianggap partikel.
Konsep partikel ini berlainan dengan desain badan kaku. Dalam gerakan bujursangkar dan gerakan parabola, contohnya, kita menganggap benda-benda dalam bentuk partikel, sebab saat bergerak, setiap bagian mempunyai kecepatan (speed linear contohnya) yang serupa. Ketika mobil bergerak, contohnya, mobil depan dan belakang mempunyai kecepatan yang sama. Hal ini memperlihatkan tag kendaraan beroda empat alias selaku partikel.
Ketika sebuah benda melakukan gerakan rotasi, kecepatan linear setiap bagian dari tubuh. Bagian dari benda-benda yang dekat dengan sumbu rotasi bergerak lebih lambat (kecepatan linier kecil), sedangkan benda-benda di tepi mobile (kecepatan linear lebih besar) lebih singkat. Jadi kita tidak mampu menilai objek sebagai partikel sebab kecepatan linear setiap bab tubuh yang berlawanan ketika berjalan. kecepatan sudut semua bab dari objek yang sama. Dalam hal ini telah diterangkan dalam kinematika rotasi.
Makara pada peluang ini, pertama di ketika peninjauan inersia sebuah partikel yang melakukan gerakan rotasi. Hal ini dimaksudkan untuk menolong kita mengetahui desain momen inersia. Setelah membahas momen inersia partikel, maka akan tahu momen inersia dari benda tegar. Tubuh kaku mempunyai bentuk dan ukuran keanekaragaman. Makara untuk membantu kita memahami momen inersia benda-benda yang memiliki bentuk dan ukuran yang berlawanan, pertama kita mesti memahami momen inersia partikel. Namun, setiap benda yang mampu dibilang berisikan partikel-partikel.
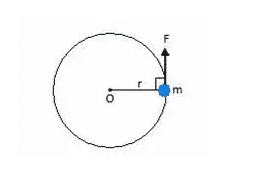
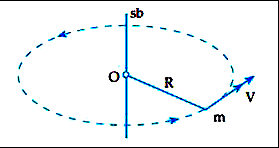
Sekarang mari kita memikirkan sebuah partikel yang melaksanakan gerakan rotasi. Dapat memakai gambar
Sebagai acuan, sebuah partikel bermassa m diberikan sebagai kekuatan F sehingga dia melaksanakan gerakan rotasi terhadap sumbu O. Partikel ialah r dari sumbu rotasi. partikel yang mulanya tetap (kecepatan = 0). Memiliki diberikan F kekuatan, partikel bergerak dengan kecepatan linear tertentu. Pada mulanya keheningan partikel, kemudian pindah (menjalani
perubahan dalam kecepatan baris) setelah gaya yang diberikan. Dalam hal ini, kecepatan tangensial keberatan. Percepatan tagensial = percepatan linear partikel pada rotasi.
Satu mampu mengungkapkan relasi antara gaya (F), massa (m) dan percepatan tangensial (at), persamaan hukum kedua Newton:
F = matan
Karena partikel yang melakukan gerakan berputar, maka pasti mempunyai percepatan sudut. Hubungan antara percepatan sudut dari percepatan tangensial dinyatakan oleh persamaan:
= Atan r.α
Sekarang kita memasuki singgung dalam persamaan di atas:
→ F = = atan Matan rα
F = mrα
Multiply kiri dan kanan oleh:
Rf = r (mrα)
Rf = mr 2
Catatan sisi kiri. Rf = torsi untuk memaksa arah tegak lurus kepada sumbu (ketimbang gambar di atas). Persamaan ini mampu ditulis selaku :
τ = (m 2) α
MR2 yakni momen massa inersia partikel m, yang berputar jauh r dari sumbu rotasi. Persamaan ini juga menawarkan korelasi antara torsi, momen inersia dan percepatan sudut partikel yang melaksanakan gerakan berputar. Kesegaran istilah hukum kedua persamaan Newton untuk partikel berputar.
Dan Momen inersia partikel, yakni produk dari massa partikel (m) dengan kuadrat jarak dari sumbu rotasi tegak lurus kepada partikel (r2). Sebagai contoh, bandingkan dengan gambar di atas. Secara matematis, momen inersia partikel dirumuskan selaku berikut:
I = m 2
Keterangan: I = momen inersia
m = massa partikel
r = jarak partikel dari sumbu rotasi
Momen Inersia Benda Tegar
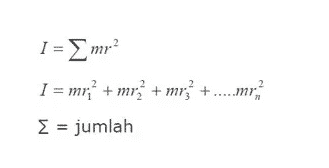
Bisakah kita berpikir tubuh kaku berisikan banyak partikel tersebar melalui itu. Setiap partikel yang tidak mempunyai massa dan pasti mempunyai jarak r dari sumbu rotasi. sehingga momen inersia setiap objek adalah total momen inersia semua partikel yang membentuk itu.
Ini cuma persamaan umum. Namun, untuk memilih momen inersia dari benda tegar, kita perlu menimbang-nimbang badan kaku saat melakukan. Meskipun bentuk dan ukuran dua benda bahu-membahu, namun jika dua benda yang berputar pada sumbu poros alias yang berlawanan, maka momen inersia juga berlainan.
I = Momen Inersia
L = Panjang Benda
M = Massa Benda
Momen Inersia Benda Pejal
Momen Inersia Stem ulet
Pertimbangkan batang tanah m dan panjang L untuk memutar sekitar sumbu yang melewati sentra massa (Gb.1). Di bagasi, ada dua variabel: massa dan panjang batang. Mengingat momen inersia batang (HDI) tergantung pada dua variabel tersebut yaitu dimensi analisis, kita bisa mendapatkan momen inersia batang proporsional seimbang dengan massa panjang poros persegi dan batang atau matematika dapat ditulis:
Rumus Momen Inersia dan cara Menghitungnya
Dibawah ini terdapat beberapa momen inersia pada titik partikel. Dalam titik partikel tersebut ada massa (m) yang melaksanakan gerak rotasi pada sumbu jari jari (R). Untuk memperhatikan perihal rumus inersia, kau bisa melihat gambar dibawah ini.
Berdasarkan gambar diatas bisa kita simpulkan bahwa momen inersia yang ditunjukkan dengan perkalian massa partikel dengan jarak partikel kuadrat menuju sumbu putar (jari jari/R). Dengan begitu ditemukan rumus momen inersia pada titik partikel yaitu:
I = m x R²
Keterangan rumus momen inersia di atas:
I = Momen Inersia (kg.m²)
m = massa partikel (kg)
R = jari jari rotasi (m)
benda yang terdiri atas susunan partikel (titik), apabila melaksanakan gerak rotasi mempunyai momen inersia sama dengan hasil jumlah dari momen inersia partikel penyusunnya.
1). mengkalkulasikan momen inersia kalau benda berotasi
jikalau benda yang berotasi adalah benda tegar yang memiliki susunan periode yang berlanjut atau tidak bisa uraikan maka momen inersia bisa dihitung dengan metode integrel sebagai berikut dibawah ini.
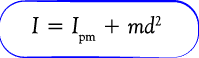
2). menjumlah momen inersia apabila sumbu putarnya tidak berada pada sentra kurun
momen inersia benda yang sumbunya berada pada sentra kurun disebut momen nersia pusat masa. jika sumbu putarnya tidak berada pada sentra masa, untuk mencari momen inersianya, mampu memakai persamaan berikut.
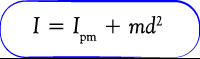
Selain rumus momen inersia diatas, ada juga tabel momen inersia untuk benda-benda yang bentuknya terorganisir dan berotasi pada sumbu tertentu. Berikut penjelasan beserta rumusnya:
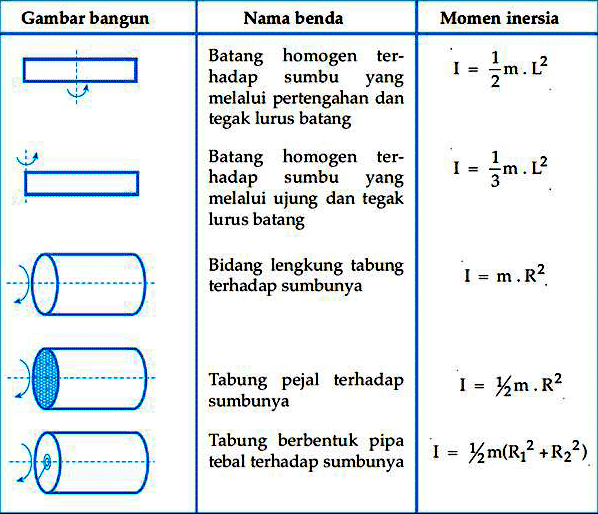

Pengertian momen inersia dan rumus momen inersia mampu kita semua terapkan dalam kehidupan sehari-hari. mirip ada suatu mobil yang melaju dengan kecepatan sarat lalu mengerem secara datang-datang. Mobil tersebut mempunyai kecenderungan untuk mempertahankan gerakannya. kemudian ada teladan inersia lain ialah kecenderungan pada benda diam.
Contoh Momen Inersia Dalam Kehidupan Sehari-hari
ada beberapa Contoh Momen Inersi Kehidupan Sehari-hari, berikut dibawah ini
1). teladan momen inersia menggunakan sepeda motor
pernahkan kau menaiki sepeda motor dengan kecepatan tinggi, lalu mengerem secara datang-tiba Nah, saat motor yang kamu naiki melaju dengan kencang, kemudian direm dengan tiba-tiba, maka pada dikala itu adanya kecenderungan sepeda motor mempertahankan geraknya.
2). contoh momen inersia pada benda diam
Apakah kecenderungan tersebut juga berlaku untuk benda membisu? acuan, letakanlah selembar kertas HVS di atas meja, lalu taruh suatu penghapus di atas kertas HVS tersebut. Tarik kertas HVS dengan segera. Apa yang terjadi? penghapus tetap tinggal di atas meja. Artinya sifat alami benda yang condong mempertahankan keadaanya yang membisu.
Penerapan Momen Inersia
terdapat beberapa contoh penerapan momen inersia,berikut penjelasannya
1). Momen Inersia Pada Pemain Ski Es
Momen Inersia yaitu sifat yang dimiliki oleh suatu benda untuk mempertahankan letaknya dari gerak berotasi. Momen inersia ialah ukuran resistansi atau kelembaman suatu benda kepada pergantian dalam gerak rotasi. Momen inersia bergantung pada distribusi massa benda relatif dengan sumbu rotasi benda.
alasannya torsi yang dijalankan oleh es yakni kecil, momentum anguler pemain ski ialah mendekati konstan. pada saat ia mempesona tangannya ke dalam ke arah badannya, momen inersia badannya terhadap sumbu vertikal lewat badannya berkurang. alasannya momentum angularnya L = I? harus tetap konstan, bila I berkurang, kecepatan angularnya ? bertambah; artinya, beliau berputar dengan laju yang lebih cepat.
2). Aplikasi Momen Inersia Pada jaw crusher
Jaw Crusher sendiri dipakai secara luas pada industri pertambangan, industri metal, konstruksi, pembangun jalan tol, pembangunan rel kereta serta industri kimia.
cara Kerja Mesin Jaw Crusher adalah Jaw Crusher bekerja mengandalkan kekuatan motor. dengan roda motor, poros eksentrik dikendalikan oleh sabuk segitiga dan slot wheel untuk menciptakan jaw plate bergerak seirama.
Demikialah postingan tentang Momen Inersia : Pengertian, Momen, Rumus, Contoh, Penerapan dari pengajar.co.id smeoga berfaedah.